MATLAB Filter Tool
Ryan McGee
RMM052000@utdallas.edu
Manual: FD_Manual.doc
ABSTRACT
The goal of this project was to create a MATLAB program to automate the design of notch filters, resonators, and oscillators.† Based on user input of desired parameters, MATLAB will generate the appropriate linear constant coefficient difference equation (LCCDE).† The LCCDE of each filter is output to the user along with a graph of the respective frequency response or waveform.
PROCEDURE
Setting the Sampling
Frequency
For each filter the user is able to specify the sampling frequency, FS, and, F0, the frequency to be notched in the case of FIR or IIR notch filters, or resonated in the case of all-pole or pole-zero resonators.† For oscillators, the user can set the sampling and oscillating frequency.† The user will be warned if FS does not exceed twice F0, for this does not satisfy the Nyquist theorem and will result in an inaccurate response.†
Setting the Gain
Additionally for the notch filters and resonators, the user is allowed to specify the gain in dB at a particular frequency of the filter (FG).† FG is normalized by the sampling frequency and converted to radians to obtain w0.† ††The default gain at FG of each filter is computed and then normalized to obtain the userís desired gain at FG.†
Obtaining the Impulse
Response
To derive an impulse response for a filter, one must first plot the zeros of the filter on the unit circle (r = 1) in the complex z-plane.† The resulting z-domain equation can be easily converted to the discrete vector and made causal by multiplying by a power of z.† The IIR notch, all-pole, and pole-zero resonator all have poles lying at the same angle as their zeros but at distance of r < 1 from the origin.† Values of r closer to 1 (closer to each zero) will result in a narrower notch or resonator.†
The derivations for each filter were done by hand and vectors containing the n-domain values were entered into MATLAB.† Also, the user is prompted to enter a value of r for each filter and given restrictions (0 ≤ r < 1).
Generating the LCCDE
I derived by hand the LCCDE from each filterís impulse response by converting from the z-domain to the discrete domain (n-domain).† I input the standard form of each LCCDE into MATLAB as a string that calls upon my impulse response vectors to obtain the proper coefficients.† The result is a neat printout of each particular filterís LCCDE based on the userís specified parameters.
The Oscillator
Specifying the gain of the oscillator is irrelevant in this case because the oscillator is a waveform generator rather than a filter.† The user is simply asked for the sampling frequency and oscillating frequency.† My program generates the appropriate waveform from the LCCDE of the oscillator.†
EXAMPLES OF RESULTS
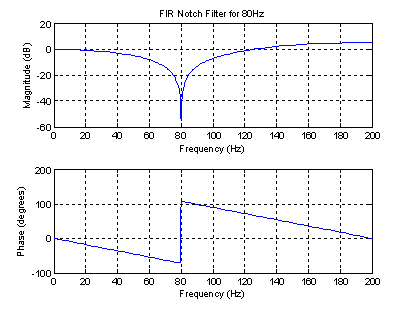
FIR Notch
|
Choose one of the following or type 999 to quit. †1. FIR Notch †2. IIR Notch †3. All-Pole Resonator †4. Pole-Zero Resonator †5. Oscillator †1 Sampling Frequency: 400 Notch Frequency: 80 Frequency to Set Gain: 0 Gain (dB) at 0Hz: 0 LCCDE = y(n) = 0.7236[1x(n) + -0.618x(n-1) + 1x(n-2)]
|
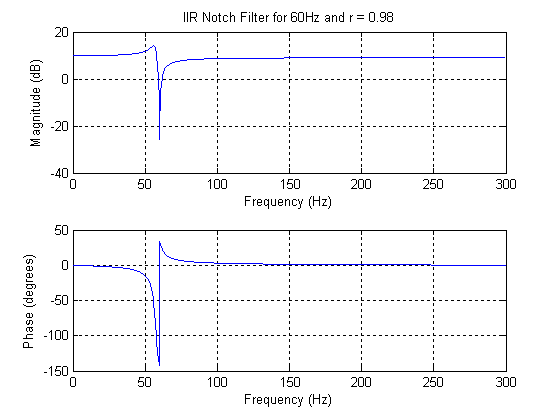
IIR Notch
|
Choose one of the following or type 999 to quit. †1. FIR Notch †2. IIR Notch †3. All-Pole Resonator †4. Pole-Zero Resonator †5. Oscillator †2 Sampling Frequency: 600 Notch Frequency: 60 r: .98 Frequency to Set Gain: 20 Gain (dB) at 20Hz: 10 LCCDE = y(n) + -1.618y(n-1) + 0.9604y(n-2) = 2.801[x(n) + 1x(n-1) + x(n-2)]
|
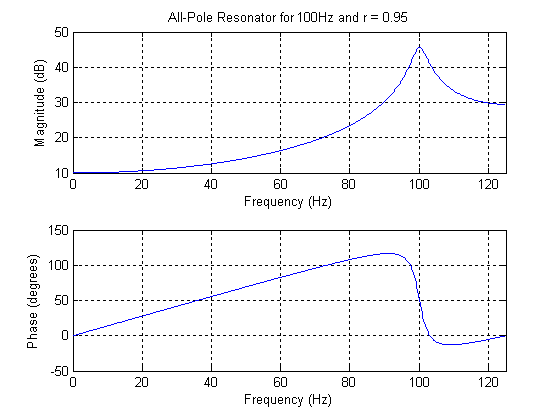
All-Pole Resonator
|
Choose one of the following or type 999 to quit. †1. FIR Notch †2. IIR Notch †3. All-Pole Resonator †4. Pole-Zero Resonator †5. Oscillator †3 Sampling Frequency: 250 Resonating Frequency: 100 r: .95 Frequency to Set Gain: 0 Gain (dB) at 0Hz: 10 LCCDE = y(n) + 1.537y(n-1) + 0.9025y(n-2) = 10.88x(n)
|
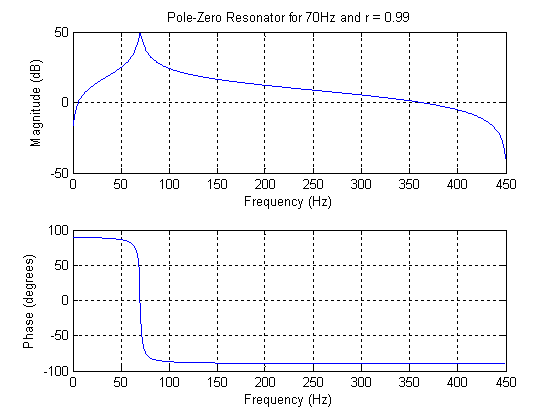
Pole-Zero Resonator
|
Choose one of the following or type 999 to quit. †1. FIR Notch †2. IIR Notch †3. All-Pole Resonator †4. Pole-Zero Resonator †5. Oscillator †4 Sampling Frequency: 900 Resonating Frequency: 70 r: .99 Frequency to Set Gain: 10 Gain (dB) at 10Hz: 5 LCCDE = y(n) + -1.748y(n-1) + 0.9801y(n-2) = 2.894[x(n) - x(n-2)]
|
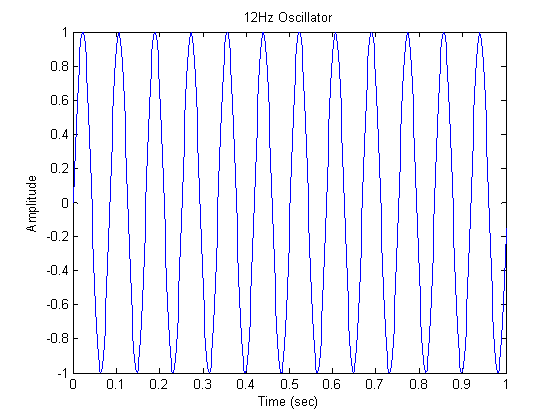
Oscillator
|
Choose one of the following or type 999 to quit. †1. FIR Notch †2. IIR Notch †3. All-Pole Resonator †4. Pole-Zero Resonator †5. Oscillator †5 Sampling Frequency: 500 Oscillating Frequency: 12 LCCDE = y(n) + -1.977y(n-1) + y(n-2) = 0.1502x(n-1)
|
CONCLUSION
While the theory behind construction of digital filters can
take some time to fully understand, it is no more difficult than the theory
behind analog filters.† However, the main
difference between analog and digital lies in the ease of implementation.† Whereas analog circuits must be physically
constructed with parts lacking perfect tolerance, digital filters and
oscillators can be more precisely constructed using relatively few lines of
code and with no cost for parts (besides a computer).†
MATLAB CODE
|
%Filter
Designer (FD.m) † choice = input('Choose one of the following or type
999 to quit.\n 1. FIR Notch \n 2. IIR Notch \n 3. All-Pole Resonator \n 4.
Pole-Zero Resonator \n 5. Oscillator \n '); † if(choice == 1) † ††† %FIR notch filter † ††† FS = input('Sampling Frequency: '); ††† F0 = input('Notch Frequency: '); ††† if (F0 > FS/2) ††††††† warnstr
=['WARNING!
The Sampling frequency is less than twice the notch frequency. Response will
be inaccurate.'] ††† end ††† FG = input('Frequency to Set Gain: '); ††† if (FG == F0) ††††††† warnstr
=['WARNING!
User should not set the gain of the notch frequency. Response will be
inaccurate.'] ††† end ††† fgstr = ['Gain (dB)
at ' num2str(FG) 'Hz: ']; ††† FGAINdB = input(fgstr); ††† FGAIN = 10^(FGAINdB/20); ††† ††† w0 = 2*pi*F0/FS; ††† wg =
2*pi*FG/FS; ††† ††† GH = abs(1 - 2*cos(w0)*exp(-j*wg) + exp(-j*2*wg)); ††† G = FGAIN/GH; ††† ††† h = [1 -2*cos(w0)
1]; ††† ††† freqz(G*h,1,[],
FS); ††† ††† titlestr = ['FIR Notch
Filter for ' num2str(F0) 'Hz']; ††† title(titlestr) ††† ††† LCCDE = ['y(n) = ' num2str(G, 4)
'[' num2str(h(1),
4) 'x(n)
+ '
num2str(h(2), 4) 'x(n-1) + ' num2str(h(3), 4) 'x(n-2)]'] † elseif(choice == 2) † ††† %IIR Notch † ††† FS = input('Sampling Frequency: '); ††† F0 = input('Notch Frequency: '); ††† if (F0 > FS/2) ††††††† warnstr
=['WARNING!
The Sampling frequency is less than twice the notch frequency. Response will
be inaccurate.'] ††† end ††† r = input('r: '); ††† if (r >= 1 || r < 0) ††††††† warnstr =['WARNING! r
should be a positive value < 1'] ††† end ††† FG = input('Frequency to Set Gain: '); ††† if (FG == F0) ††††††† warnstr
=['WARNING!
User should not set the gain of the notch frequency. Response will be
inaccurate.'] ††† end ††† fgstr = ['Gain (dB)
at ' num2str(FG) 'Hz: ']; ††† FGAINdB =
input(fgstr); ††† FGAIN = 10^(FGAINdB/20); ††† ††† w0 = 2*pi*F0/FS; ††† wg =
2*pi*FG/FS; ††† ††† bg = abs(1 - 2*cos(w0)*exp(-j*wg) + exp(-j*2*wg)); ††† ag = abs(1 - 2*cos(w0)*exp(-j*wg) +
(r^2)*exp(-j*2*wg)); ††† GH = bg/ag; ††† G = FGAIN/GH; ††† ††† b = [1 -2*cos(w0)
1]; ††† a = [1 -2*cos(w0)
(r^2)]; ††† ††† freqz(G*b,a,1024,
FS); ††† titlestr = ['IIR Notch
Filter for ' num2str(F0) 'Hz and r = ' num2str(r)]; ††† title(titlestr) ††† ††† LCCDE = ['y(n) + ' num2str(b(2),
4) 'y(n-1)
+ '
num2str((r^2), 4) 'y(n-2) = ' num2str(G, 4) '[x(n) + ' num2str(b(1),
4) 'x(n-1)
+ x(n-2)]'] † elseif(choice == 3) † ††† %All-Pole Resonator † ††† FS = input('Sampling Frequency: '); ††† F0 = input('Resonating Frequency: '); ††† if (F0 > FS/2) ††††††† warnstr
=['WARNING!
The Sampling frequency is less than twice the resonating frequency. Response
will be inaccurate.'] ††† end ††† r = input('r: '); ††† if (r >= 1 || r < 0) ††††††† warnstr =['WARNING! r
should be a positive value < 1'] ††† end ††† FG = input('Frequency to Set Gain: '); ††† fgstr = ['Gain (dB)
at ' num2str(FG) 'Hz: ']; ††† FGAINdB =
input(fgstr); ††† FGAIN = 10^(FGAINdB/20); ††† ††† wr =
2*pi*F0/FS; ††† if (r >= 0.9) ††††††† w0 = wr; ††† else ††††††† w0 = acos((2*r*cos(wr))/(1 + r^2)); ††† end ††† ††† wg =
2*pi*FG/FS; ††† ††† ag = abs(1 -
2*r*cos(w0)*exp(-j*wg) +
(r^2)*exp(-j*2*wg)); ††† GH = 1/ag; ††† G = FGAIN/GH; ††† ††† a = [1 -2*r*cos(w0)
(r^2)]; † ††† freqz(G,a,[], FS); ††† titlestr = ['All-Pole
Resonator for ' num2str(F0) 'Hz and r = ' num2str(r)]; ††† title(titlestr) † ††† LCCDE = ['y(n) + ' num2str(a(2),
4) 'y(n-1)
+ '
num2str((r^2), 4) 'y(n-2) = ' num2str(G, 4) 'x(n)'] ††† elseif(choice == 4) † ††† %Pole-Zero Resonator † ††† FS = input('Sampling Frequency: '); ††† F0 = input('Resonating Frequency: '); ††† if (F0 > FS/2) ††††††† warnstr
=['WARNING!
The Sampling frequency is less than twice the resonating frequency. Response
will be inaccurate.'] ††† end ††† r = input('r: '); ††† if (r >= 1 || r < 0) † ††††††warnstr =['WARNING! r
should be a positive value < 1'] ††† end ††† FG = input('Frequency to Set Gain: '); ††† if (FG == 0) ††††††† warnstr
=['WARNING!
User should not set the DC (0Hz) gain. Response will be inaccurate.'] ††† end ††† fgstr = ['Gain (dB)
at ' num2str(FG) 'Hz: ']; ††† FGAINdB =
input(fgstr); ††† FGAIN = 10^(FGAINdB/20); ††† ††† wr =
2*pi*F0/FS; ††† if (r >= 0.9) ††††††† w0 = wr; ††† else ††††††† w0 = acos((2*r*cos(wr))/(1 + r^2)); ††† end ††† ††† wg =
2*pi*FG/FS; ††† ††† bg = abs(1 - exp(-j*2*wg)); ††† ag = abs(1 -
2*r*cos(w0)*exp(-j*wg) +
(r^2)*exp(-j*2*wg)); ††† GH = bg/ag; ††† G = FGAIN/GH; ††† ††† b = [1 0 -1]; ††† a = [1 -2*r*cos(w0)
(r^2)]; ††† ††† freqz(G*b,a,[], FS); ††† titlestr = ['Pole-Zero
Resonator for ' num2str(F0) 'Hz and r = ' num2str(r)]; ††† title(titlestr) ††† ††† LCCDE = ['y(n) + ' num2str(a(2),
4) 'y(n-1)
+ '
num2str((r^2), 4) 'y(n-2) = ' num2str(G, 4) '[x(n) - x(n-2)]'] † elseif (choice == 5) %Oscillator † ††† FS = input('Sampling Frequency: '); ††† F0 = input('Oscillating Frequency: '); ††† if (F0 > FS/2) ††††††† warnstr
=['WARNING!
The Sampling frequency is less than twice the oscillating frequency. Waveform
will be inaccurate.'] ††† end ††† ††† w0 = 2*pi*F0/FS; ††† ††† b = [0 sin(w0)]; ††† a = [1 -2*cos(w0)
1]; †† ††† LCCDE = ['y(n) + ' num2str(a(2),
4) 'y(n-1)
+ y(n-2) = ' num2str(b(2), 4) 'x(n-1)'] ††† ††† x(1) = 1; ††† x(2) = 0; ††† y(1) = 0; ††† y(2) = sin(w0)*x(1); ††† for n = 3:FS; ††††††† x(n) = 0; ††††††† y(n) = 2*cos(w0)*y(n-1)
- y(n-2) + sin(w0)*x(n-1); ††† end † ††† t0 = 1:FS; ††† t = t0/FS; ††† plot(t, y) ††† titlestr =
[num2str(F0) 'Hz Oscillator']; ††† title(titlestr) ††† xlabel('Time (sec)') ††† ylabel('Amplitude') † elseif (choice == 999) ††† %do nothing and quit else ††† ††† 'Invalid Input.† Please enter a valid integer choice, 1-5 or
type 999 to quit.' ††† FD() † end ††† if (choice ~=
999) ††† clear all ††† FD() end † clear all |